문제

어떤 동물원에 가로로 두칸 세로로 N칸인 아래와 같은 우리가 있다.

이 동물원에는 사자들이 살고 있는데 사자들을 우리에 가둘 때, 가로로도 세로로도 붙어 있게 배치할 수는 없다. 이 동물원 조련사는 사자들의 배치 문제 때문에 골머리를 앓고 있다.

동물원 조련사의 머리가 아프지 않도록 우리가 2*N 배열에 사자를 배치하는 경우의 수가 몇 가지인지를 알아내는 프로그램을 작성해 주도록 하자. 사자를 한 마리도 배치하지 않는 경우도 하나의 경우의 수로 친다고 가정한다.

입력

첫째 줄에 우리의 크기 N(1≤N≤100,000)이 주어진다.

출력

첫째 줄에 사자를 배치하는 경우의 수를 9901로 나눈 나머지를 출력하여라.

다이내믹 프로그래밍 문제다. 가장 어려웠던 건, 점화식을 구하는 일이었다.

규칙을 찾아 점화식을 세우면 코드 짜는 건 어렵지 않다. 특히 다이내믹 프로그래밍에선 점화식이 더욱 중요한 듯.

한참을 생각해봐도 잘 모르겠다. 문제 설명 자체도 좀 이해하기 어렵게 서술돼 있다. 결국 다른 사람들이 푼 방식을 뒤졌다. 여러 방법 중 가장 이해하기 쉽고 깔끔하게 정리한 글을 발견했다. 역시 세상은 넓고, 고수는 많다.

위 블로그 글도 충분히 이해하기 쉽게 설명했지만, 나같은 초보 배우미 분들을 위해 좀 더 쉽게 정리해보았다.

먼저, 문제에서…

사자를 한 마리도 배치하지 않는 경우도 하나의 경우의 수로 친다고 가정하자.

이 말을 처음엔 이해하지 못했다. 즉 아예 사자를 배치하지 않는 경우도 1로 친다는 건데,

dp란 리스트를 만든다고 할 때 dp[0]은 곧 한 줄도 없는 경우를 일컫는다. 이 경우에도 경우의 수는 1이다. 한 줄도 없으니 당연히 사자도 한 마리도 배치할 수 없지만, 그래도 경우의 수는 1이다.

dp[1] 즉 가로 두 칸 1줄을 배치했을 때의 경우의 수는 3이다. ① 한 마리도 배치하지 않는 경우, ② 왼쪽 칸에만 배치하는 경우, ③ 오른쪽 칸에만 배치하는 경우다. 아래 그림처럼.

이제 줄이 2개 이상일 경우에 대해 각각의 경우의 수를 따져보면 된다.

1. 두 번째 줄(n = 2)에 사자를 한 마리도 배치하지 않는 경우

   이 경우 첫째 줄에 사자를 한 마리도 배치하지 않거나, 왼쪽에 배치하거나, 오른쪽 칸에 배치하는 경우가 생긴다. dp[1] 즉 dp_i-1의 경우와 같다. (파란색 음영 부분 참조)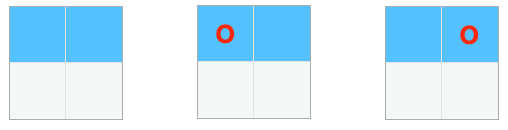

   

2. 첫 번째 줄(n = 1)에 사자를 한 마리도 배치하지 않는 경우

   이 경우 사자를 두 번째 줄 오른쪽 칸 또는 왼쪽 칸에 배치해야 한다. 첫 번째 줄은 두 경우 모두 비어 있다. 완전히 비어 있는 경우는 dp[0] 즉 dp_i-2이다. 따라서 이 경우는 dp_i-2 × 2다.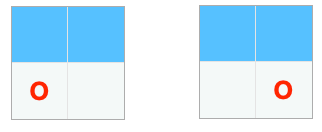

   

3. 첫 번째 줄(n = 1)과 두 번째 줄(n = 2)에 모두 사자를 배치하는 경우

   이 경우 파란색 음영 부분을 보면 사자를 왼쪽에 배치한 경우와 사자를 오른쪽 칸에 배치한 경우, 즉 경우의 수는 2다. 이는 dp[1](dp_i-1)에서 dp[0](dp_i-2)를 뺀 경우와 같다.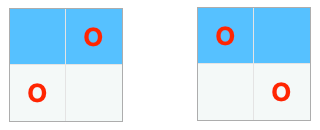

   

   

n번째 줄이 주어졌을 때 경우의 수, 즉 dp_i는 위 3가지 경우를 합했을 때의 값이다.

dp_i = dp_i-1 + (dp_i-2 × 2) + (dp_i-1 - dp_i-2) = dp_i-1× 2 + dp_i-2

점화식이 만들어졌으니 코드를 짜보자.

n = int(input())
dp = [1] * (n+1) # 값 1이 n+1개 만큼 들어 있는 리스트(dp) 생성
dp[1] = 3
for i in range(2, n+1):
    if n == 1:
        print(dp[1])
    else:
        dp[i] = dp[i-1]*2 + dp[i-2]
        dp[i] = dp[i] % 9901
print(dp[n])

여기서 주의할 건, dp[i]를 구할 때마다 %9901를 실행해 넣어줘야 한다는 점이다. 일단 값을 넣어두고 나중에 프린트할 때 %9901을 실행하면 십중팔구 시간초과에 걸린다. dp[i] 값을 입력하는 과정에서 오버플로우가 발생하기 때문이다.

[문제 보기]